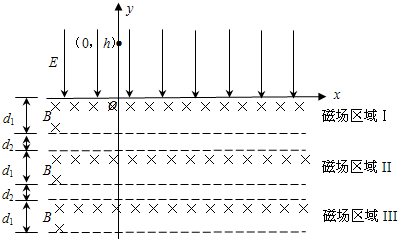
如图所示，磁感应强度为B的条形匀强磁场区域的宽度都是d1，相邻磁场区域的间距均为d2，x轴的正上方有一电场强度大小为E，方向与x轴和B均垂直的匀强电场区域，将质量为m、带正电量为q的粒子（重力忽略不计）从y轴上坐标为h处由静止释放．求：
（1）粒子在磁场区域做匀速圆周运动的轨道半径．
（2）若粒子经磁场区域I、II后回到x轴，则粒子从开始释放经磁场后第一次回到x轴需要的时间和位置坐标．
（3）若粒子从y轴上坐标为H处以初速度v0沿x轴正方向水平射出，此后运动中最远能到达第k个磁场区域的下边缘，并再次返回到x轴，求d1、d2的值．
（1）、设粒子进入磁场时的速度为v，粒子在电场中做加速运动，由功能关系有：
qEh=
mv2…①1 2
粒子在磁场中做圆周运动，有：
R=
…②mv qB
①②两式联立得：
R=2mEh qB2
（2）、设粒子在电场中的加速时间为t1，则有：
h=1 2 Eq m
，得t1=t 21 2mh Eq
设粒子在磁场中的运动时间为t2，则t2=
T，T=1 2
，则可得：2πm qB
t2=πm qB
设粒子在无磁场区域的运动时间为t3，则t3=
，2d2 vcosα
又因cosα=R2- d 21 R
将v、R代入t3=
，得：2d2 vcosα
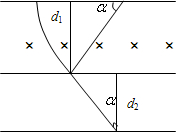
t3=2md2 2mEqh-B2 q2d 21
则运动的时间为：
t=t1+t2+t3=
+2mh qE
+πm qB 2md2 2mEqh-B2 q2d 21
设粒子回到x轴的坐标为x，则有：
x=2R+2d2tanα
解得：x=2
+2mEh qB2
．2d1d2
-2mEh qB2 d 21
（3）粒子在电场中类平抛，进入磁场时速度v2，则有：
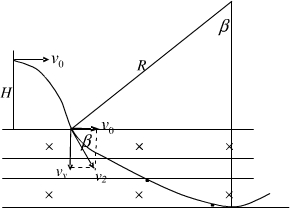
v2=
，且有vy=v 20 +v 2y 2EqH m
v2与水平方向的夹角有：cosβ=v0 v2
粒子在磁场中偏转半径为：R=mv2 qB
因粒子最远到达第k个磁场区域的下边缘，有：
kd1=R（1-cosβ）
解得：d1=
．m(
)
+v 20
-v02EqH m kqB
粒子在无磁场区域做匀速直线运动，故d2可以取任意值．
答：（1）粒子在磁场区域做匀速圆周运动的轨道半径为
．2mEh qB2
（2）粒子从开始释放经磁场后第一次回到x轴需要的时间为
+2mh qE
+πm qB
，位置坐标为22md2 2mEqh-B2 q2d 21
+2mEh qB2
．2d1d2
-2mEh qB2 d 21
（3）若粒子从y轴上坐标为H处以初速度v0沿x轴正方向水平射出，此后运动中最远能到达第k个磁场区域的下边缘，并再次返回到x轴，d1的值为
，d2可以取任意值．m(
)
+v 20
-v02EqH m kqB