问题
问答题
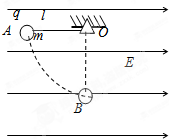
如图所示,在场强为E的匀强电场中,一绝缘轻质细杆l可绕点O点在竖直平面内自由转动,另一端有一个带正电的小球,电荷量为q,质量为m,将细杆从水平位置A自由释放运动至最低点B处的过程中:
(1)请说明电势能如何变化?变化了多少?
(2)求出小球在最低点时的动能?
(3)求在最低点时绝缘杆对小球的作用力?
答案
(1)因为由A到B过程中电场力做正功,所以电势能减小.减小的电势能等于电场力做功:△EP=W=qEl
(2)小球运动到最低点的过程中,重力和电场力做功,由动能定理得:mgl+qEl=
mv2-01 2
EK=
mv2=mgl+qEl1 2
(3)整理得:v=
,即小球在最低点的速率.2(mg+qE)l m
在最低点由牛顿第二定律得:T-mg=mv2 l
将v代人公式,整理得:T=3mg+2Eq
故最低点绝缘杆对小球的作用力T=3mg+2Eq.
答::(1)电势能减小.减小的电势能等于电场力做功为W=qEl
(2)小球运动到最低点的动能为mgl+qEl
(3)在最低点时绝缘杆对小球的作用力为3mg+2Eq.
