问题
问答题
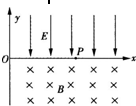
如图所示,在x轴上方有一匀强电场,场强大小为E,方向竖直向下.在x轴下方有一匀强磁场,磁感应强度为B,方向垂直于纸面向里.在x轴上有一点p,离原点距离为a.现有一带电量为+q,质量为m的粒子,不计重力,从0<x<a区间某点由静止开始释放后,能经过p点.试求:
(1)释放瞬间粒子的加速度;
(2)释放点的坐标x、y应满足的关系式?
答案
(1)要使粒子从静止开始能经过P点,其初始位置必须在匀强电场区域里,根据牛顿第二定律得:
释放瞬间粒子的加速度为a=
,方向沿y轴负方向.qE m
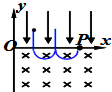
(2)由于粒子从0<x<a区间某点由静止开始释放,轨迹如图.
由于粒子可能偏转一个、十个…半圆到达P点,由几何知识得
a-x=2nR(n=1,2,3,…)①
设释放处距O的距离为y,则有
qEy=
mv2 ②1 2
又 qvB=m
③v2 R
联立①②③得 y=
(n=1,2,3,…)B2q(a-x)2 8n2mE
答:
(1)释放瞬间粒子的加速度为
,方向沿y轴负方向.qE m
(2)释放点的坐标x、y应满足的关系式y=
(n=1,2,3,…).B2q(a-x)2 8n2mE
