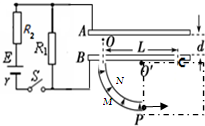
如图所示,电源电动势E=60V,内阻r=1Ω,R1=3Ω,R2=6Ω.间距d=0.03m的两平行金属板A、B水平放置,闭合开关S,两板之间存在着匀强电场.在B板上开有两个间距为L=1.2m的小孔.M、N为两块同心1/4圆弧形金属板,圆心都在贴近B板的O′处,两板间的距离很近,两板上端的中心线正对着B板上的小孔(与B板的间隙可忽略不计),下端切线水平,P点恰好在O′的正下方,两圆弧形金属板间的电场强度可认为大小处处相等,方向都指向O′.现从正对B板小孔紧靠A板的O处由静止释放一个质量为m=1.0×10-5Kg、电量为q=1×10-3C的带正电微粒(微粒的重力不计),问:
(1)微粒穿过B板小孔时的速度多大;
(2)为了使微粒能在MN板间运动而不碰板,MN板间的电场强度大小应满足什么条件;
(3)从释放微粒开始,经过多长时间微粒通过两圆弧形金属板?
(4)为了让P点出射的带电粒子能射到B板的右侧C点小孔,现在P点外侧虚线框内另加一个竖直方向的有界匀强电场,则电场强度E为多少?
(1)因为平行金属板和电阻R1并联,故根据闭合电路欧姆定律可得:
UAB=
E=R1 R1+R2+r
60V=18V3 3+6+1
根据动能定理,粒子通过AB过程中电场力对粒子做的功等于粒子动能的变化:
qUAB=
mv2-01 2
得粒子获得的速度v=
=2qUAB m
m/s=60m/s.2×1×10-3×18 1.0×10-5
(2)粒子以v=60m/s进入MN电场,在电场力作用下沿轨道做匀速圆周运动,根据题意知轨道的半径R=
=0.6m,电场力提供圆周运动的向心力L 2
qEMN=m
得v2 R
MN间电场强度EMN=
=mv2 qR
N/C=60N/C.1.0×10-5×602 1.0×10-3×0.6
(3)粒子在AB间做初速度为0的匀加速直线运动,粒子受到电场力F=q
,粒子产生的加速度a=UAB d
,则粒子通过AB所用的时间qUAB md
t1=
=2d a
=2d qUAB md
=2md2 qUAB
s=10-3s2×1.0×10-5×0.032 1.0×10-3×18
当粒子从O到P刚好经过
圆周,已知粒子圆周运动的线速度v=60m/s,半径R=0.6m,可知,粒子运动时间1 4
t2=
=
×2πR1 4 v
s=0.016s
×2×3.14×0.61 4 60
则粒子从释放到通过两圆弧形金属板所需的时间t=t1+t2=0.001+0.016s=0.017s.
(4)因为从P点射出是粒子速度v=60m/s在水平方向,为使粒子落在右侧C点,在区域中加入竖直向上的匀强电场,使得粒子在水平方向以v=60m/s做匀速直线运动,在竖直方向粒子在电场力作用下做初速度为0的匀加速直线运动,根据题意粒子落在C点的过程中,粒子在水平和竖直方向的位移均为
=0.6m,令所加电场为EL 2
则有:竖直方向加速度a=
,水平方向位移为0.6m,速度为60m/s,则有:qE m
vt= L 2
at2=1 2 L 2
即:vt= L 2
×1 2
t2=qE m L 2
代入数据可解得:E=120N/C.
答:(1)微粒穿过B板小孔时的速度为60m/s;
(2)为了使微粒能在MN板间运动而不碰板,MN板间的电场强度大小应满足EMN=60N/C;
(3)从释放微粒开始,经过0.017s微粒通过两圆弧形金属板;
(4)为了让P点出射的带电粒子能射到B板的右侧C点小孔,现在P点外侧虚线框内另加一个竖直方向的有界匀强电场,则电场强度E为120N/C.
