有一xOy平面，在x＜0的空间内，存在场强为E、与y轴成θ角的匀强

问题问答题

有一xOy平面，在x＜0的空间内，存在场强为E、与 y轴成θ角的匀强电场，如图所示．在第Ⅲ象限某处有质子源s，以某一初速度垂直于电场的方向射出质量为m、电荷量为q的质子．初速度的延长线与x轴的交点P的坐标为（-d，0），质子射出电场时恰经过坐标原点O，并沿x轴正向进入x＞0区域．在x＞0一侧有边界为圆形的匀强磁场，磁感应强度为B，方向垂直于xOy平面向外，边界某处与y轴相切．质子进入磁场被偏转，在射出磁场后垂直于电场方向回到x＜0的区域．

（1）试求出质子的初速度v₀，并确定质子源s位置的坐标．

（2）圆形磁场的最小半径r．

（3）质子从射入磁场到再次回到x＜0的电场区域所经历的时间t．

答案

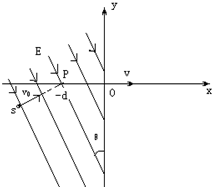
（1）设质子在电场中的运动时间为t₁，粒子垂直射入电场，在电场中偏转做类平抛运动，画出粒子的运动轨迹，根据平抛运动的推论可知，速度方向的反向延长线通过水平位移的中点，则

dcosθ=

v₀t_{1
tanθ=
qE
m
t1
v0
解得：v0=
2qEd(cosθ)2
msinθ
根据几何关系得：
x_s=-d[1+（cosθ）²]
y_s=-dsinθcosθ
质子源s位置的坐标为（-d[1+（cosθ）²]，-dsinθcosθ）．
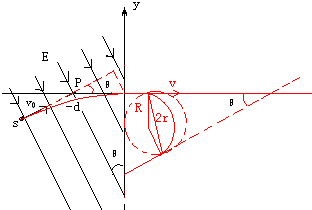
（2）设质子在磁场中运动轨迹的半径为R，画出粒子的运动轨迹如图所示，
则根据几何关系有：
r=Rcos
θ
2
Bqv=
mv2
R
，
v=
v0
cosθ
=
2qEd
msinθ
解得：
r=
1
B
2qEd
msinθ
cosθ
2
（3）设在磁场中运动的时间为t₂，从出磁场到y轴的时间为t₃，则
t=t₂+t₃
其中t₂=
π-θ
2π
T=(π-θ)m
Bq

t3=
r+rsinθ
2
vcosθ
=m(1+sinθ
2
)
qBcosθ
cosθ
2
所以t=t₂+t₃=
m
qB
[π-θ+(1+sinθ
2
)cosθ
2
cosθ
]
答：（1）质子的初速度v₀，为
2qEd(cosθ)2
msinθ
，质子源s位置的坐标为（-d[1+（cosθ）²]，-dsinθcosθ）．
（2）圆形磁场的最小半径r为
1
B
2qEd
msinθ
cosθ
2
．
（3）质子从射入磁场到再次回到x＜0的电场区域所经历的时间t为
m
qB
[π-θ+(1+sinθ
2
)cosθ
2
cosθ
]．}