如图，有位于竖直平面上的半径为R的圆形光滑绝缘轨道，其上半部

问题问答题

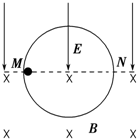
如图，有位于竖直平面上的半径为R的圆形光滑绝缘轨道，其上半部分处于竖直向下、场强为E的匀强电场中，下半部分处于垂直水平面向里的匀强磁场中；质量为m，带正电，电荷量为q的小球，从轨道的水平直径的M端由静止释放，若小球在某一次通过最低点时对轨道的压力为零，求：

（1）磁感应强度B的大小；

（2）小球对轨道最低点的最大压力；

（3）若要小球在圆形轨道内做完整的圆周运动，求小球从轨道的水平直径的M端下滑的最小速度．

答案

（1）设小球向右通过最低点时的速率为v，由题意得：

mgR=

mv²…①

qBv-mg=m

…②

3mg

2gR

．…③

（2）小球向左通过最低点时对轨道的压力最大．

F_N-mg-qBv=m

…④

F_N=6mg．…⑤

（3）要小球完成圆周运动的条件是在最高点满足：

mg+qE=m

…⑥

从M点到最高点由动能定理得：

-mgR-qER=

…⑦

由以上可得v₀=

3R(mg+qE)

…⑧

答案：（1）磁感应强度B的大小为

3mg

2gR

，

（2）小球对轨道最低点的最大压力为6mg，

（3）小球从轨道的水平直径的M端下滑的最小速度为

3R(mg+qE)

．