如图所示，OA、OB两根绳子系着一个质量为m=0.5Kg的小球，两绳的A

问题问答题

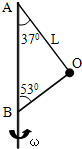
如图所示，OA、OB两根绳子系着一个质量为m=0.5Kg的小球，两绳的A、B端分别固定在竖直转动轴上，OA绳长L=2m，两绳都拉直时与轴的夹角分别为37⁰和53⁰，（sin37°=0.6 cos37°=0.8 g=10m/s²）求：

（1）小球随轴转动的角速度ω=2.4rad/s时，绳OA、OB的张力分别是多少？

（2）小球随轴转动的角速度ω=3.0rad/s时，绳OA、OB的张力分别是多少？

答案

（1）若OB绳子刚好伸直，则：

mgtan37°=m（Lsin37°）ω₀²

解得：ω₀=2.5rad/s

当ω=2.4rad/s＜ω₀时，OB绳子是弯曲的；

故OB绳子张力为零；

根据牛顿第二定律，有：

T_OAx=m（Lsin37°）ω²=3.456N；

T_OAy=mg=5N；

TOA=

2OAx

2OAy

≈6.1N；

（2）当ω=3.0rad/s＞ω₀时，OB绳子是伸直的，根据牛顿第二定律，有

水平方向：T_OAcos37°-T_OBcos53°-mg=0

竖直方向：T_OAsin37°+T_OBcos37°=m（Lsin37°）ω²

解得：T_OA=7.24N

T_OB=1.32N

（1）小球随轴转动的角速度ω=2.4rad/s时，绳OA的张力是6.1N，OB的张力为零；

（2）小球随轴转动的角速度ω=3.0rad/s时，绳OA的张力是7.24N，OB的张力为1.32N．