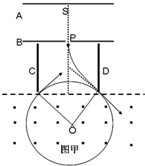
带电粒子在AB两极板间靠近A板中央附近S处静止释放,在两极板电压中加速,从小孔P平行CD极板方向的速度从CD极板中央垂直进入偏转电场,B板靠近CD板的上边缘如图甲.在CD两板间加如图乙所示的交变电压,设t1=0时刻粒子刚好进入CD极板,t2=t0时刻粒子恰好从D板的下边缘飞入匀强磁场,匀强磁场的上边界与CD极板的下边缘在同一水平线上,磁场范围足够大,加速电场AB间的距离,偏转电场CD间的距离及CD极板长均为d,图象乙中t0和U0都为已知,带电粒子重力不计,不考虑电场和磁场边界影响.求:

(1)加速电压U=?U0=?
(2)带电粒子进入磁场时的速度?
(3)若带电粒子在t3时刻刚好从C极板的下边缘进入偏转电场,并刚能返回到初始位置S处,t3=?,t0=?
(4)带电粒子全程运动的周期T=?
(1)设带电粒子进入偏转电场时的速度为v0,从偏转电场中射出的速度为v,t1=0时刻粒子刚好进入CD极板,t2=t0时刻粒子恰好从D板的下边缘飞入匀强磁场,
即由几何关系可知:
v=
v0①2
在加速电场中,有动能定理得:
qU=1 2
②mv 20
在偏转电场中,有
qU0=1 2
mv2-1 2 1 2
③mv 20
所以,U=
U0 1 2
(2)由于粒子在偏转电场中做类平抛运动,带电粒子进入磁场时的速度大小为:
v=
v0=2
④
d2 t0
速度方向和磁场边界成45°角.
(3)带电粒子在磁场中,洛伦兹力提供向心力,故:
qvB=
⑤mv2 R
而,T=
⑥2πR v
且在磁场中运动时间为:t=
⑦3T 4
由几何关系得:R=
d⑧2 2
由题意得:t=t3-t0⑨
由④⑤⑥⑦⑧⑨得,t3=(1+
)t03π 4
(4)带电粒子全程运动的周期为:T总=2(
)+2×2d v0
+d v0
=6t0+3T 4
t03π 4
答:(1)加速电压U=
U01 2
(2)带电粒子进入磁场时的速度
,速度方向和磁场边界成45°角
d2 t0
(3)若带电粒子在t3时刻刚好从C极板的下边缘进入偏转电场,并刚能返回到初始位置S处,t3=(1+
)t03π 4
(4)运动全程的时间6t0+
t03π 4
