问题
选择题
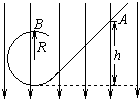
一个带负电荷q,质量为m的小球,从光滑绝缘的斜面轨道的A点由静止下滑,小球恰能通过半径为R的竖直圆形轨道的最高点B而做圆周运动.现在竖直方向上加如图所示的匀强电场,若仍从A点由静止释放该小球,则( )
A.小球不能过B点
B.小球仍恰好能过B点
C.小球能过B点,且在B点与轨道之间压力不为0
D.以上说法都不对
答案
A、B,没有电场时,最高点速度设为v
则 mg=mv2 R
又根据机械能守恒定律
mg(h-2R)=
mv2m1 2
解得h=
R5 2
加上电场时,恰好过最高点需要的速度设为v′
则mg-qE=m
v′=v′2 R (mg-qE)R m
而由动能定理,得
mg(h-2R)-qE(h-2R)=
mv′2,v′=1 2 (mg-qE)R m
说明小球仍恰好能过B点.故A错误,B正确.
C、由上,小球仍恰好过最高点,球与轨道间无作用力.故C错误
D、D错误
故选B
