如图甲所示，一半径R=1.4m、圆心角等于143°的竖直圆弧形光滑轨

问题问答题

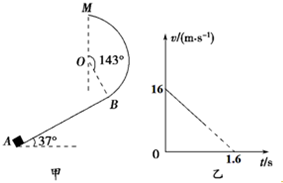
如图甲所示，一半径R=1.4m、圆心角等于143°的竖直圆弧形光滑轨道，与斜面相切于B处，圆弧轨道的最高点为M，斜面倾角θ=37°，t=0时刻有一物块沿斜面上滑，其在斜面上运动的速度变化规律如图乙所示．若物块恰能达到M点，（取g=10m/s2，sin37°=0.6，cos37°=0.8），求：

（1）物块经过B点时的速度v_B；

（2）物块与斜面间的动摩擦因数μ；

（3）AB间的距离x．

答案

（1）设物体的质量为m，由于物体恰能到达M点，

则在M点有

=mg

物体从B到M点的过程，

由动能定理有：-mgR(1+cos37°)=

，

联立以上两式可得，vB=

4.6gR

=8m/s

（2）由v-t图可知，物体在从A到B点的运动过程中的加速度为a=10m/s²

由牛顿第二定律有，-（mgsin37°+μmgcos37°）=ma

物体与斜面间的动摩擦因数为μ=

-(a+gsin37°)

gcos37°

=0.5

（3）物体在从A到B的运动过程中，

初速度v_A=16m/s，

由运动学公式

=2ax

解得：x=

=9.6m

答：（1）物块经过B点时的速度8m/s；

（2）物块与斜面间的动摩擦因数0.5；

（3）AB间的距离9.6m．