问题
问答题
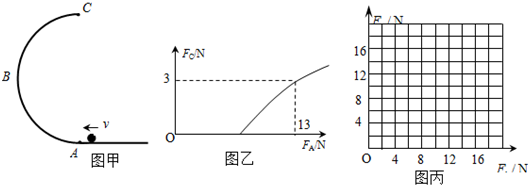
如图甲,ABC为竖直放置的半径为0.1m的半圆形轨道,在轨道的最低点和最高点A、C各安装了一个压力传感器,可测定小球在轨道内侧,通过这两点时对轨道的压力FA和FC.质量为0.1kg的小球,以不同的初速度v冲入ABC轨道.(g取10m/s2)
(1)若FC和FA的关系图线如图乙所示,求:当FA=13N时小球滑经A点时的速度vA,以及小球由A滑至C的过程中损失的机械能;
(2)若轨道ABC光滑,小球均能通过C点.试推导FC随FA变化的关系式,并在图丙中画出其图线.
答案
(1)由牛顿第三定律可知,小球在A、C两点所受轨道的弹力大小NA=FA,NC=FC
在A点,由牛顿第二定律得:NA-mg=
…①m v 2A R
解得vA=2
m/s…②3
在C点,由牛顿第二定律得:NC+mg=
…③m v 2C R
对A至C的过程,由动能定理得:Wf-mg•2R=
m1 2
-v 2C
m1 2
…④v 2A
①②③联立得Wf=
m1 2
-v 2C
m1 2
+2mgR=v 2A
(2mg-FA+FC)R+2mgR…⑤1 2
解得Wf=-0.2J…⑥
故损失的机械能为0.2J
(2)因轨道光滑,小球由A至C的过程中机械能守恒,则有
m1 2
=v 2A
m1 2
+mg•2R…⑦v 2C
联立①③⑥得NA-NC=6mg
即FC=FA-6N…⑧
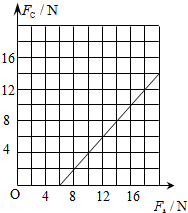
图线如右图所示…⑨
答:(1)当FA=13N时小球滑经A点时的速度vA为2
m/s,小球由A滑至C的过程中损失的机械能是0.2J;3
(2)FC随FA变化的关系式为FC=FA-6N,在图丙中画出其图线如图所示.
