问题
问答题
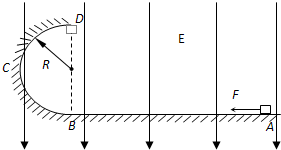
如图所示,AB为水平轨道,A、B间距离s=1m,BCD是半径为R=0.2m的竖直半圆形轨道,B为两轨道的连接点,D为轨道的最高点,整个轨道处于竖直向下的匀强电场中,场强大小为E=103N/C.一带正电q=5×10-3C的小物块质量为m=0.5kg,它与水平轨道间的动摩擦因数均为μ=0.1.小物块在F=10N的水平恒力作用下从A点由静止开始运动,到达B点时撤去力F,小物块刚好能到达D点,试求:(g=10m/s2)
(1)撤去F时小物块的速度大小;
(2)在半圆形轨道上小物块克服摩擦力做的功.
答案
(1)从A到B过程中,由动能定理可得:
Fs-μ(mg+qE)s=
mv2-0,解得:v=6m/s;1 2
(2)在D点,由牛顿第二定律得:mg+qE=m
,v 2D R
从B到D过程中,由动能定理可得:-2qER-2mgR-Wf=
mvD2 -1 2
mv2,1 2
解得:Wf=4J;
答:(1)撤去F时小物块的速度大小为6m/s;
(2)在半圆形轨道上小物块克服摩擦力做的功为4J.
