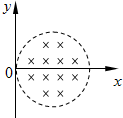
如图所示,圆形区域的匀强磁场,磁感应强度为B、方向垂直纸面向里,边界跟y轴相切于坐标原点O.O点处有一放射源,沿纸面向各方向射出速率均为V的某种带电粒子,带电粒子在磁场中做圆周运动的半径是圆形磁场区域半径的两倍.已知该带电粒子的质量为m、电量为+q,不考虑带电粒子的重力.
(1)磁场区域的半径为多少?
(2)在匀强磁场区域内加什么方向的匀强电场,可使沿Ox方向射出的粒子不发生偏转,强场为多少?
(3)若粒子与磁场边界碰撞后以原速率反弹,则从O点沿x轴正方向射入磁场的粒子第一次回到O点经历的时间是多长?(已知arctan2=
)7π 20
(1)由BqV=m
得:V2 R
R=
,mV Bq
由题意得R场=
R=1 2
;mV 2Bq
(2)加-y方向匀强电场
由 BqV=qE,
得E=BV;
(3)相邻碰撞点之间的圆弧对应的圆心角α有:tan
α=1 2
=2R R场
即α=
;7π 20
要使粒子碰撞后返回O点,应有k1α=2πk2(k1、k2为整数)
易知第一次返回O点:k1=20,k2=7(即碰撞了20次转了7周第一次回到O点)
故 t=20△t=20
T=π-α 2π
;6πm Bq
答:(1)磁场区域的半径为
;(2)电场为BV;(3)从O点沿x轴正方向射入磁场的粒子第一次回到O点经历的时间是mV 2Bq
.6πm Bq
