问题
问答题
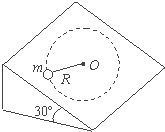
如图所示,在倾角为30°的光滑斜面上的O点钉有一根与斜面垂直的钉子,细绳的一端拴在钉子上,绳的另一端拴一个质量为m=0.2kg的小球,绳与斜面平行,小球球心到钉子的距离为R=0.8m.现使小球在斜面上做R为半径的圆周运动,则小球通过最高点时的最小速度大小为______m/s,如果细绳所能承受的最大拉力是10N,则小球通过最低点时的最大速度大小为______m/s.( 重力加速度g=10m/s2)
答案
对小球进行受力分析,在最高点绳子拉力恰好为零时,速度取最小值,根据向心力公式则有:
mgsin30°=mv2 R
解得:v=
=2m/sgsin30°R
在最低点,合力提供向心力,当绳子拉力取最大值时,速度取最大值,根据向心力公式得:
T-mgsin30°=mv2 R
解得:vmax=
m/s=6m/s36
故答案为:2;6
