问题
计算题
如图所示，在某空间建立一坐标xoy，其间充满着x正方向的匀强电场，场强E =2.0V/m和垂直xoy平面向外的匀强磁场，磁感强度B=2.5T。今有一带负电微粒质量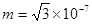
kg，电量q=-5×10-7 C。在该空间恰能做匀速直线运动。求：
（1）试分析该题中重力可否忽略不计（需通过计算说明）。
（2）该微粒运动的速度。
（3）若该微粒飞经y轴的某点M时，突然将磁场撤去而只保留电场，则微粒将再次经过y轴的N点，则微粒从M到N运动的时间为多长，M、N两点间的距离为多大？（图中M、N在坐标上未标出）
答案
（1）重力不能忽略不计；（2）1.6m/s； 与y轴负方向成60º角；（3）s=1.536m
题目分析: （1） 根据已知条件可计算出电场力：F=qE=5×10-7×2.0N=1.0×10-6N
重力：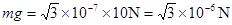
重力与电场力在同一个数量级——所以重力不能忽略不计。
（2）该微粒运动的速度。由于微粒恰好作直线运动，所以合力为0。微粒受重力、电场力和洛仑兹力如图示：
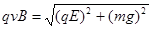
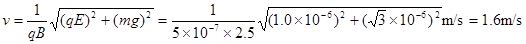由图可得速度方向与y轴负方向成θ角，满足
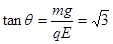， 所以：θ=60º
（3）用运动的合成与分解的方法将速度v沿重力方向和沿电场力反方向分解的来求M、N两点间的距离。其解答过程如下：
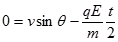
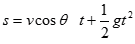
由上述两式联立可得运动时间t=0.48s，M、N两点间的距离s=1.536m。
该题也可以选择用类似于斜面上的平抛运动来求M、N两点间的距离。将s分解为沿v方向的s cosθ和垂直v方向的s sinθ，则： scosθ= vt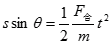 
由上述两式联立可得运动时间t=0.48s，M、N两点间的距离s=1.536m。