问题
问答题
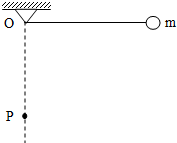
如图,摆线长L,摆球质量m,将摆球拉至与悬点O等高处由静止释放,在O点的正下方有一口钉子P,OP=
L,求:3 4
(1)摆球摆至最低点时的速度?
(2)悬线与钉子接触前瞬间悬线的拉力?
(3)摆球绕着钉子在竖直平面内摆到最高点时的速度多大?
答案
(1)根据动能定理得,mgL=
mv21 2
解得v=
.2gL
(2)根据牛顿第二定律得,T-mg=mv2 L
解得T=3mg.
(3)根据机械能守恒定律得,mg
+L 2
mv′2=1 2
mv21 2
解得v′=gL
小球恰好到达最高点的临界速度mg=m
,解得v0=v02 L 2 gL 2
因为
>gL
,所以小球能够到达最高点,到达最高点的速度为gL 2
.gL
答:(1)摆球摆至最低点的速度为
.2gL
(2)悬线与钉子接触前瞬间绳的拉力为3mg.
(3)摆球绕着钉子在竖直平面内摆到最高点时的速度为
.gL
