问题
计算题
如图所示，在以O为圆心，半径为R=10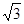
cm的圆形区域内，有一个水平方向的匀强磁场，磁感应强度大小为B2=0.1T，方向垂直纸面向外。M、N为竖直平行放置的相距很近的两金属板， S1、S2为M、N板上的两个小孔，且S1、S2跟O点在垂直极板的同一水平直线上。金属板M、N与一圆形金属线圈相连，线圈的匝数n=1000匝，面积S=0.2m2，线圈内存在着垂直纸面向外的匀强磁场，磁感应强度大小随时间变化的规律为B1=B0+kt（T），其中B0、k为常数。另有一水平放置的足够长的荧光屏D，O点跟荧光屏D之间的距离为H=2R。比荷为2×105 C/kg的正离子流由S1进入金属板M、N之间后，通过S2向磁场中心射去，通过磁场后落到荧光屏D上。离子的初速度、重力、空气阻力及离子之间的作用力均可忽略不计。问：
（1）k值为多少可使正离子垂直打在荧光屏上
（2）若k=0.45T/s，求正离子到达荧光屏的位置。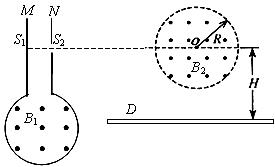
答案
(1) 
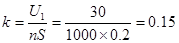T/s （2
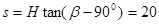cm
(1) 正离子被AK之间的电场加速以速度v1进入磁场后做1/4圆离开磁场垂直打在荧光屏上，则半径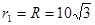
cm ， （1分）
由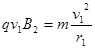
（2分）
又有：
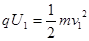（2分）
由以上两式可得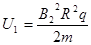
=30V （1分）
根据法拉第电磁感应定律，得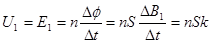
（2分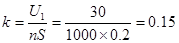）T/s （1分）
(2) 
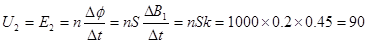V 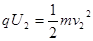（2分）
（2分）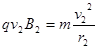 
， （2分）
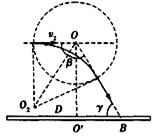
解得：r2=30cm （1分）
正离子进入磁场后的径迹如图所示，由几何知识可得
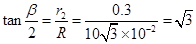，即
（1分）
所以，正离子到达荧光屏的位置B距中点O/的距离为
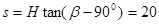cm （1分）
综合考查了电磁场中粒子的运动，根据公式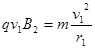和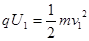可算处加速电场电压，根据法拉第电磁感应定律，得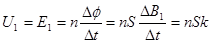可得出k值。第二问先算出加速电场的电压，然后根据洛伦兹力公式，算出半径，根据几何知识算出正离子到达荧光屏的位置B距中点O/的距离