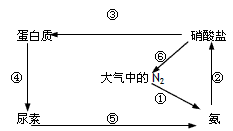
问题
计算题
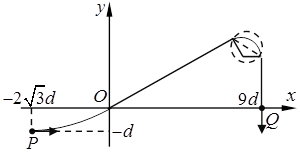
(18 分)如图所示,在平面直角坐标系第Ⅲ象限内充满+y 方向的匀强电场, 在第Ⅰ象限的某个圆形区域内有垂直于纸面的匀强磁场(电场、磁场均未画出);一个比荷为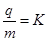 的带电粒子以大小为 v 0的初速度自点
的带电粒子以大小为 v 0的初速度自点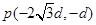 沿+x 方向运动,恰经原点O进入第Ⅰ象限,粒子穿过匀强磁场后,最终从 x轴上的点 Q(9 d,0 )沿-y 方向进入第Ⅳ象限;已知该匀强磁场的磁感应强度为
沿+x 方向运动,恰经原点O进入第Ⅰ象限,粒子穿过匀强磁场后,最终从 x轴上的点 Q(9 d,0 )沿-y 方向进入第Ⅳ象限;已知该匀强磁场的磁感应强度为 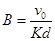 ,不计粒子重力。
,不计粒子重力。
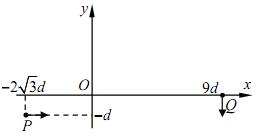
(1)求第Ⅲ象限内匀强电场的场强E的大小;
(2) 求粒子在匀强磁场中运动的半径R及时间t B;
(3) 求圆形磁场区的最小半径rm。
答案
(1)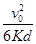 (2)
(2)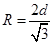
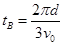 (3)d
(3)d
题目分析:⑴粒子在第Ⅲ象限做类平抛运动:
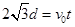 ①
①
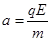 ②
②
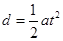 ③
③
解得:场强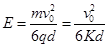 ④
④
(2)设粒子到达O点瞬间,速度大小为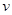 ,与
,与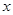 轴夹角为
轴夹角为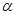 :
:
 ⑤
⑤
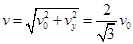 ⑥
⑥
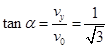 ,
,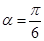 ⑦
⑦
粒子在磁场中,洛伦兹力提供向心力:
 ⑧
⑧
解得,粒子在匀强磁场中运动的半径
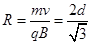 ⑨
⑨
在磁场时运动角度:
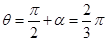 ⑩
⑩
在磁场时运动时间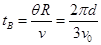 (11)
(11)
(3)如图,若粒子进入磁场和离开磁场的位置恰位于磁场区的某条直径两端,可求得磁场区的最小半径
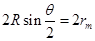 (12)
(12)
解得: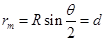 (13)
(13)