问题
问答题
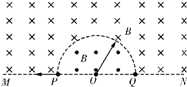
如图所示,直线MN下方无磁场,上方空间存在两个匀强磁场,其分界线是半径为R的半圆,两侧的磁场方向相反且垂直于纸面,磁感应强度大小都为B.现有一质量为m、电荷量为q的带负电粒子从P点沿半径方向向左侧射出,最终打到Q点,不计粒子的重力.求:
(1)粒子从P点到Q点的最短运动时间及其对应的运动速率;
(2)符合条件的所有粒子的运动时间及其对应的运动速率.
答案
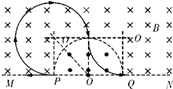
(1)粒子的运动轨迹将磁场边界分成2等分时,对应有最短运动时间
由几何知识可得:粒子运动的半径r=R
又Bv0q=m
得v0=v 20 R BqR m
由对称性可得,粒子刚好在磁场中运动一周t=2πm Bq
(2)设粒子的运动轨迹将磁场边界分成n等分(n=2,3,4…)
由几何知识得 θ=
,r=Rtanθ(n=2,3,4…) π 2n
粒子的速率为v0=
tanBRq m
(n=2,3,4…)π 2n
当n为偶数时,由对称性可得粒子在磁场中运动圈,t=
T=π 2
(n=2,4,6…)π2m Bq
当n为奇数时,t为周期的整数倍加上第一段的运动时间,即
t=
T+n-1 2
T=π+ π n 2π
(n=3,5,7…)(n2+1)πm nBq
