问题
问答题
如图所示,长为L的细绳,一端系有一质量为m的小球,另一端固定在O点,细绳能够承受的最大拉力为9mg.现将小球拉至细绳呈水平位置,然后由静止释放,小球将在竖直平面内摆动,不计空气阻力.求:
(1)小球通过O点正下方时,小球对绳的拉力.
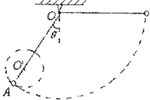
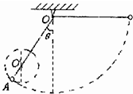
(2)如果在竖直平面内直线OA(OA与竖直方向的夹角为θ)上某一点O′钉一个小钉,为使小球可绕O′点在竖茸水平面内做完整圆周运动,且细绳不致被拉断,OO′的长度d所允许的范围.
答案
(1)设小球在O点正下方时的速度为v1,绳的拉力为F,由机械能守恒定律得:
mgL=mv02 2
在最低点 F-mg=m v 21 L
解得 F=3mg
由牛顿第三定律得,小球对绳的拉力大小F′=3mg,方向竖直向下.
(2)设小球绕O点在竖直面内做完整圆周运动的半径为r,恰能过最高点时速度为v2,
则:mg=m v 22 r
解得 v2=rg
由水平到最高点,由动能定理:mg(Lcosθ-rcosθ-r)=
m1 2 v 22
解得r=
L 2cosθ 3+2cosθ
因绳能承受的最大拉力为Tm=9mg,设小球在小圆轨道最低点的速度为v3,
由向心力公式得:Tm-mg=m v 23 r
由动能定理得:mg(Lcosθ-rcosθ+r)=
m1 2 v 23
解得 r=
Lcosθ 3+cosθ
所以r的取值范围:
L≤r≤cosθ 3+cosθ
L2cosθ 3+2cosθ
由于d=L-r,所以有
L≤d≤3 3+2cosθ
L3 3+cosθ
答:(1)小球通过O点正下方时,小球对绳的拉力为3mg.
(2)d所允许的范围为
L≤d≤3 3+2cosθ
L.3 3+cosθ
