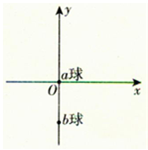
在光滑绝缘的水平面(纸面)上建有如图所示的平面直角坐标系,在此水平面上可视为质点的不带电小球a静止于坐标系的原点O,可视为质点的带正电小球b静止在坐标为(0,-h)的位置上.现加一方向沿y轴正方向、电场强度大小为E、范围足够大的匀强电场,同时给a球以某一速度使其沿x轴正方向运动.当b球到达坐标系原点O时速度为v0,此时立即撤去电场而改加一方向垂直于纸面向外、磁感应强度大小为B、范围足够大的匀强磁场,最终b球能与a球相遇.求:
(1)b球的比荷
;q m
(2)从b球到达原点O开始至b球与a球相遇所需的时间;
(3)撤去电场时,a球的位置坐标.
(1)b球在电场力作用下加速,由动能定理得:qEh=
m1 2 v 20
则b球的比荷为
=q m v 20 2Eh
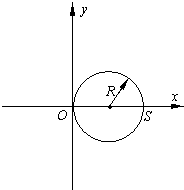
(2)b球运动到原点后,只在磁场力作用下,在水平面上做匀速圆周运动,有:qv0B=mv 20 R
得:R=mv0 qB
b球圆周运动的周期为 T=
=2πR v0
=2πm qB 4πhE B v 20
b球只能与a球相遇在图中的S处,相遇所需时间为:
t=(k+
)T=(k+1 2
)1 2
,(k=1,2,3,…) 4πhE B v 20
(3)a球从O点开始运动到S点,与b球相遇所用时间为:t′=t1+t
由h=
t1得:t1=v0 2 2h v0
a球通过的位移为:OS=2R
由v=2R t1+t
可得a球的速度为:v=2Ev0 Bv0+(2k+1)πE
则撤去电场时,a球在x轴上的坐标为:x0=vt1=4Eh Bv0+(2k+1)πE
球的位置为(
,0)(k=1,2,3,…)4Eh Bv0+(2k+1)πE
答:(1)b球的比荷
为q m
;v 20 2Eh
(2)从b球到达原点O开始至b球与a球相遇所需的时间是
,(k=1,2,3,…);4πhE B v 20
(3)撤去电场时,a球的位置坐标是(
,0)(k=1,2,3,…).4Eh Bv0+(2k+1)πE
