如图a所示,两竖直线所夹区域内存在周期性变化的匀强电场与匀强磁场,变化情况如图b、c所示,电场强度方向以y轴负方向为正,磁感应强度方向以垂直纸面向外为正。t=0时刻,一质量为m、电量为q的带正电粒子从坐标原点O开始以速度v0沿x轴正方向运动,粒子重力忽略不计,图b、c中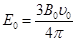 ,
,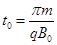 ,B0已知.要使带电粒子在0~4nt0(n∈N)时间内一直在场区运动,求:
,B0已知.要使带电粒子在0~4nt0(n∈N)时间内一直在场区运动,求:
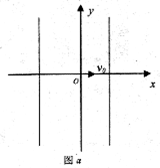
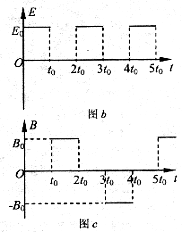
(1) 在给定的坐标上画出带电粒子在0~4t0时间内的轨迹示意图,并在图中标明粒子的运动性质;
(2) 在t0时刻粒子速度方向与x轴的夹角;
(3) 右边界到O的最小距离;
(4) 场区的最小宽度。
(1)见解析;(2)与x轴成370夹角;(3)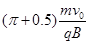 ;(4)
;(4)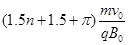
题目分析:(1)(5分)
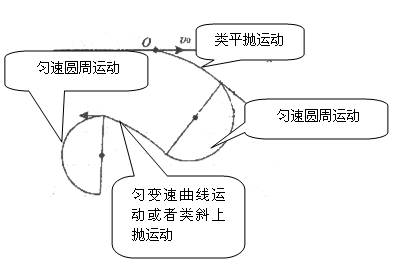
评分说明:图正确1分,运动性质每个1分。
(2)粒子做类平抛运动
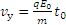 (1分)
(1分)
又 (1分)
(1分)
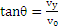 (1分)
(1分)
则t0时刻粒子速度方向与x轴的夹角为37〬(1分)
(3)如图所示:
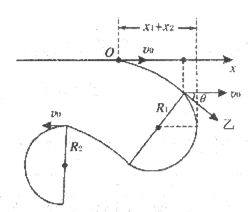
粒子作类平抛运动的水平位移
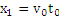 (1分)
(1分)
有几何关系可知 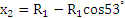 (1分)
(1分)
根据牛顿第二定律 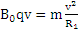 (1分)
(1分)
其中 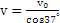 (1分)
(1分)
右边界到O点的距离最小值为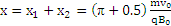 (1分)
(1分)
(4)每隔时间4t0,粒子向左平移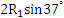 (1分)
(1分)
4nt0时刻,粒子与O点在x方向相距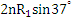 (1分)
(1分)
根据牛顿第二定律 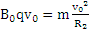 (1分)
(1分)
则左侧场区边界离O点的距离为
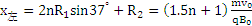 (2分)
(2分)
故在0~4nt0时间内,场区的宽度至少为
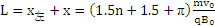 (1分)
(1分)

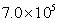 Pa)以内,但有些司机,为了获取更多利益,肆意超载。有一辆自重3t的6轮货车,核准载货量为4t,实际装货9t,如果每个车轮与路面的接触面积为0.02m2,每个车轮平均分担所有负重。(g取10N/kg)
Pa)以内,但有些司机,为了获取更多利益,肆意超载。有一辆自重3t的6轮货车,核准载货量为4t,实际装货9t,如果每个车轮与路面的接触面积为0.02m2,每个车轮平均分担所有负重。(g取10N/kg)