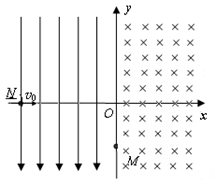
如图所示,在xoy平面内的y轴左侧有沿y轴负方向的匀强电场,y轴右侧有垂直纸面向里的匀强磁场,y轴为匀强电场和匀强磁场的理想边界。一个质量为m、电荷量为q的带正电粒子(不计重力)从x轴上的N点(-L,0)以v0沿x轴正方向射出。已知粒子经y轴的M点(0,-L/2)进入磁场,若匀强磁场的磁感应强度为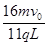 .求:
.求:
(1)匀强电场的电场强度E的大小;
(2)若粒子离开电场后,y轴左侧的电场立即撤去,通过计算判断粒子离开磁场后到达x轴的位置是在N点的左侧还是右侧?
(3)若粒子离开电场后,y轴左侧的电场立即撤去。要使粒子能回到N点,磁感应强度应改为多少?
(1)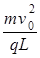 (2)粒子到达N点的右侧;(3)
(2)粒子到达N点的右侧;(3)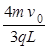
题目分析:(1) 粒子在电场中做类平抛运动,有:
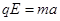 ①
①
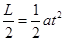 ②
②
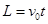 ③
③
由①②③可:
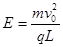 ④
④
(2)设粒子到M点的速度大小为v,方向与x轴正方向成θ角。粒子在磁场中做圆周运动的半径为R,粒子从y轴上A点离开磁场。
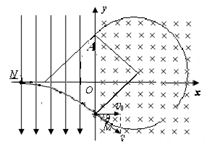
则有: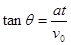 ⑤
⑤
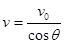 ⑥
⑥
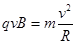 ⑦
⑦
由几何关系知,MA的距离为:  ⑧
⑧
联立②③⑤⑥⑦可得: 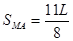 ⑨
⑨
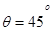 ⑩
⑩
可知A点的坐标为(0,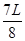 ),根据对称性在A点的速度方向与y轴负方向成
),根据对称性在A点的速度方向与y轴负方向成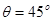 ,粒子离开磁场后做匀速直线运动,粒子到达x轴上
,粒子离开磁场后做匀速直线运动,粒子到达x轴上 位置。所以粒子到达N点的右侧。
位置。所以粒子到达N点的右侧。
(3)要使粒子回到N点,粒子须在y轴上的B点离开在磁场。设新磁场的磁感应强度大小为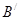 ,在磁场中做圆周运动的半径为r,则有:
,在磁场中做圆周运动的半径为r,则有:
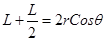 (11)
(11)
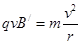 (12)
(12)
联立⑥⑩(11)(12)可解得: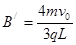 (13)
(13)
