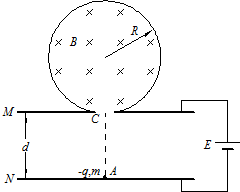
如图所示,在半径为R的绝缘圆筒内有匀强磁场,方向垂直纸面向里,圆筒正下方有小孔C与平行金属板M、N相通.两板间距离为d,两板与电动势为E的电源连接,一带电量为-q、质量为m的带电粒子(重力忽略不计),开始时静止于C点正下方紧靠N板的A点,经电场加速后从C点进入磁场,并以最短的时间从C点射出.已知带电粒子与筒壁的碰撞无电荷量的损失,且碰撞后以原速率返回.求:
(1)筒内磁场的磁感应强度大小;
(2)带电粒子从A点出发至重新回到A点射出所经历的时间.
(1)带电粒子从C孔进入,与筒壁碰撞2次再从C孔射出经历的时间为最短.
由 qE=
mv2 1 2
粒子由C孔进入磁场,在磁场中做匀速圆周运动的速率为
v=2qE m
由 r=mv qB
即Rcot30°=mv qB
得 B=1 R 2mE 3q
(2)粒子从A→C的加速度为
a=qE md
由 d=
at12,粒子从A→C的时间为1 2
t1=
=d2d a 2m qE
粒子在磁场中运动的时间为
t2=
T=1 2 πm Bq
将(1)求得的B值代入,
得 t2=πR3m 2Eq
解得 t=2t1+t2=2d
+πR2m qE
=3m 2Eq
(2m qE
d+2
πR)6 2
答:(1)筒内磁场的磁感应强度大小B=1 R
;2mE 3q
(2)带电粒子从A点出发至重新回到A点射出所经历的时间为
(2m qE
d+2
πR).6 2
