问题
计算题
（18分）如图所示，在xOy平面内存在均匀、大小随时间周期性变化的磁场和电场，变化规律分别如图乙、丙所示（规定垂直纸面向里为磁感应强度的正方向、沿y轴正方向电场强度为正）。在t=0时刻由原点O发射初速度大小为vo，方向沿y轴正方向的带负电粒子。
已知v0、t0、B0，粒子的比荷为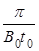
，不计粒子的重力。求：
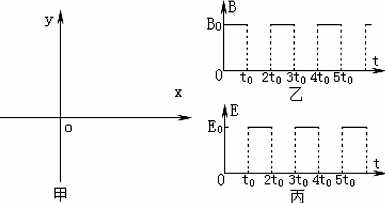
（1） t= t0时，求粒子的位置坐标；
（2）若t=5t0时粒子回到原点，求0～5to时间内粒子距x轴的最大距离；
（3）若粒子能够回到原点，求满足条件的所有E0值。
答案
(1) （
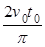，0）；(2) 
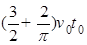(3) 
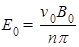（n=1，2，3，…）
题目分析：（1）由粒子的比荷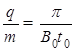
，则粒子做圆周运动的周期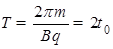
则在0-t0内转过的圆心角α=π
由牛顿第二定律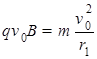
得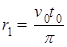
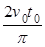位置坐标（，0）
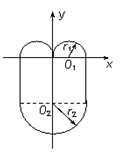
（2）粒子t=5t0时回到原点，轨迹如图所示
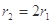
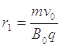
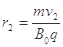
得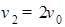
又，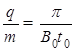 
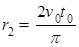
粒子在t0-2t0时间内做匀加速直线运动， 2t0-3t0时间内做匀速圆周运动，则在5t0时间内粒子距x轴的最大距离：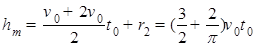
（3）如图所示，设带电粒子在x轴上方做圆周运动的轨道半径为r1，在x轴下方做圆周运动的轨道半径为r2，由几何关系可知，要使粒子经过原点，则必须满足:
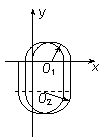
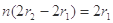（n=1，2，3，…）
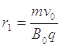
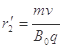
联立以上解得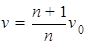
又由于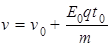
得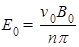（n=1，2，3，…）