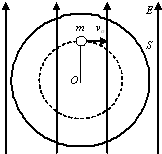
在光滑水平面上固定一个竖直圆筒S,圆筒内壁光滑(如图所示为俯视图),半径为1m.圆筒圆心O处用一根不可伸长的长0.5m的绝缘细线系住一个质量为0.2kg,电量为+5×10-5C的小球,小球体积忽略不计.水平方向有一匀强电场E=4×104N/C,方向如图所示.小球从图示位置(细线和电场线平行)以vo=10m/s垂直于场强方向运动.当细线转过900时,细线突然断裂.求:
(1)细线断裂时小球的速度大小;
(2)小球碰到圆筒内壁后不反弹,沿圆筒内壁继续做圆周运动中的最小速度值;
(3)现在圆心O处用一根牢固的不可伸长的长为0.5m的绝缘细线系住小球(小球质量和带电量均不变),小球从原图示位置以初速度10m/s垂直于场强方向运动,为保证小球接下来的运动过程中细线都不松弛,电场强度E的大小范围(场强方向不变).

(1)根据动能定理得,-Eqr=
mv12-1 2
mv021 2
解得v1=3
m/s=9.49m/s.10
(2)根据动能定理得-
Eqr=3
mv22-1 2
mv121 2
解得v2=
m/s=8.53m/s,90-10 3
则贴着内壁运动的速度v3=v2•sin300,
根据动能定理得,-EqR(1-cos300)=
mv42-1 2
mv321 2
解得v4=
m/s=3.94m/s 5+15 3 2
(3)讨论:情况一:从图示位置细线转过900,小球速度减为0:-E1qr=0-
mvo2⇒E1=1 2
=4×105N/Cmvo2 2qr
情况二:从图示位置细线转过1800:小球有最小速度,根据牛顿第二定律得,qE=mvmin2 r
解得小球速度:vmin=
,E2qr m
-E2q•2r=
mvmin2-1 2
mvo2⇒E2=1 2
=1.6×105N/C,mvo2 5qr
所以:E≤1.6×105N/C或E≥4×105N/C.
答:(1)细线断裂时小球的速度大小为9.49m/s.
(2)小球碰到圆筒内壁后不反弹,沿圆筒内壁继续做圆周运动中的最小速度值为3.94m/s.
(3)为保证小球接下来的运动过程中细线都不松弛,电场强度E的大小范围E≤1.6×105N/C或E≥4×105N/C.
