如图所示，半径分别为R和r的甲、乙两个光滑的圆形轨道置于同一竖

问题问答题

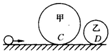
如图所示，半径分别为R和r的甲、乙两个光滑的圆形轨道置于同一竖直平面上（R＞r），两圆形轨道之间用一条水平粗糙轨道CD连接，轨道CD与甲乙两个圆形轨道相切于C、D两点．现有一小球以一定的速度先滑上甲轨道，绕行一圈后通过轨道CD再滑上乙轨道，绕行一圈后离开乙轨道．已知小球在甲轨道最高点处对轨道的压力等于球的重力，在乙轨道运动时恰好能过最高点．小球与轨道CD间的动摩擦系数为μ，求

（1）小球过甲、乙轨道的最高点时的速度V₁、V₂

（2）水平CD段的长度L．

答案

（1）设小球质量为m，当小球在甲轨道最高点时对轨道的压力等于球的重力，

由牛顿第二定律得：

N+mg=m

V₁=

2gR

当小球在乙轨道最高点时恰好能过最高点，由牛顿第二定律得：

mg=m

V₂=

（2）小球从甲轨道最高点运动到乙轨道最高点的过程中，

由动能定理得：

mg（2R-2r）-fL=

mv₂²-

mv₁^{2
滑动摩擦力f=μN=μmg
∴L=
6R-3r
2μ
答：（1）小球过甲、乙轨道的最高点时的速度分别是
2gR
，
gr．
（2）水平CD段的长度L是
6R-3r
2μ
．}