如图BCD为一半径为R的光滑圆弧面的一部分,C为圆弧的最低点,BD的连线与水平地面平行,∠BOD=106°,AB与圆弧BCD相切于B点,DE与圆弧BCD相切于D点.今将一质量为m的小物块(可视为质点)从F点由静止释放,已知FB两点间距离为5R,小物块与AB、DE间的动摩擦因数均为
,当地的重力加速度为g.(取sin53°=1 3
,cos53°=4 5
)求:3 5
(1)小物块第一次经过B点时的速度;
(2)小物块第一次经过C点时对C点的压力;
(3)小物块在AB段和DE段经历的总路程之和.
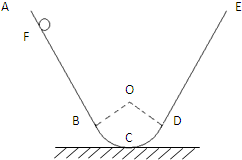
(1)由题意知,根据几何角度,可得斜面倾角为θ=53°
小物块,在斜面上,受力分析:重力G、支持力F、滑动摩擦力f,
由力的分解可得:f=μmgcosθ
从F到B,由动能定理
可得:mg×5R×sin53°-μmgcos53°×5R=
m1 2 v 2B
解之得:vB=6gR
(2)小物块,从B点到C点,由动能定理得
mg×(R-cos53°R)=
m1 2
-v 2C
m1 2
(1)v 2B
小物块,在C点,受力分析,
则有:F-mg=m
(2)v 2C R
由(1)(2)可联立解得:F=
mg39 5
(3)只有当小物块到达B点或D点的速度为零时,将只会在BCD间来回往复运动.
因而,小物块,从F点到B点(或D点),由动能定理,
则有:mg•5R×sin53°-μmgcos53°×L=0-0
解得:L=20R
答:(1)小物块第一次经过B点时的速度
; 6gR
(2)小物块第一次经过C点时对C点的压力
mg;39 5
(3)小物块在AB段和DE段经历的总路程之和为20R.
