图1所示为一根竖直悬挂的不可伸长的轻绳,下端栓一小物块A,上端固定在C点且与一能测量绳的拉力的测力传感器相连.已知有一质量为m0的子弹B沿水平方向以速度v0射入A内(未穿透),接着两者一起绕C点在竖直面内做圆周运动.在各种阻力都可忽略的条件下测力传感器测得绳的拉力F随时间t的变化关系如图2所示.已知子弹射入的时间极短,且图2中t=0为A、B开始以相同速度运动的时刻.根据力学规律和题中(包括图)提供的信息,对反映悬挂系统本身性质的物理量(例如A的质量)及A、B一起运动过程中的守恒量,你能求得哪些定量的结果?
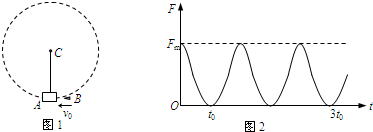
由图2可直接看出,A、B一起做周期性运动,运动周期为T=2t0.用m、m0分别表示A、B的质量,l表示绳长,v1、v2分别表示它们在圆周最低、最高点的速度,F1、F2分别表示运动到最低、最高点时绳的拉力大小;
子弹射入木块过程,根据动量守恒定律,有
m0v0=(m+m0)v1 ①
根据牛顿定律有:
最低点 F1-(m+m0)g=(m+m0)
②v 21 l
最高点 F2+(m+m0)g=(m+m0)
③v 22 l
由机械能守恒又有:
(m+m0)g•(2l)=
(m+m0)v12-1 2
(m+m0)v22 ④1 2
由图2知,F2=0,F1=Fm,由以上各式解得,反映系统本身性质的物理量是
木块质量 m=
-m0Fm 6g
细线长度 l=
g36 m 20 v 20 5 F 2m
以最低点所在的水平面为参考平面,系统总机械能是
E=
(m+m0)v12 ⑤1 2
解得
E=3 m 20
gv 20 Fm
故可以求出A的质量为
-m0,细线长度为Fm 6g
g,A、B一起运动过程中的守恒量为机械能,以最低点所在的水平面为参考平面,总机械能为36 m 20 v 20 5 F 2m
.3 m 20
gv 20 Fm
