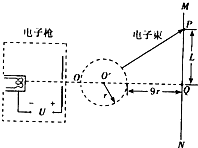
如图所示为电视机中显像管的原理示意图,电子枪中的灯丝因加热而逸出电子,这些电子再经加速电场加速后,从O点进入由磁偏转线圈产生的圆形匀强磁场区域中,经过偏转磁场后打到荧光屏MN上,使荧光屏发出荧光形成图象.磁场方向垂直于圆面,磁场区域的中心为O′,半径为r.当不加磁场时,电子束将通过O′点打到荧光屏的中心Q点.已知电子的质量为m,电量为e,加速电压为U,磁场区域的最右端到荧光屏的距离为9r.不计从灯丝逸出的电子的初速度和电子之间的相互作用.
(1)电子飞出电场时的速度为多大?
(2)荧光的亮度与电子对荧光屏的冲击有关.当不加偏转磁场时,电子束射到荧光屏中心Q点,设电子全部被荧光屏吸收,则每个电子以多大的冲量冲击荧光屏?
(3)偏转磁场的强弱会影响电子偏离荧光屏中心的距离.当加偏转磁场且磁感应强度B=1 r
时,电子束将射到荧光屏上的P点,则PQ间距L为多少?2mU 3e
(1)设电子射出电场时的速度为v,根据动能定理有:eU=
mv2;1 2
解得:v=
;2Ue m
(2)以电子为研究对象,根据动量定理有:I=0-mv;
解得:I=
;2meU
根据牛顿第三定律,电子对荧光屏的冲量大小为I,=I=
;2meU
(3)电子在磁场中做匀速圆周运动,洛伦兹力充当向心力,根据牛顿第二定律有:Bev=m
;v2 R
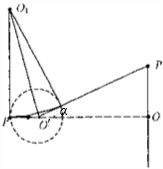
电子在磁场中偏转的半径R和r有以下关系:tan
=α 2
;r R
同时tanα=
;L 10r
代入 B=1 r
;2mU 3e
解得:L=10
r;3
答:(1)电子飞出电场时的速度为
;2Ue m
(2)每个电子以
的冲量冲击荧光屏;2meU
(3)PQ间距L为10
r.3
