问题
问答题
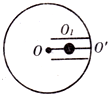
如图所示,在水平圆盘上有一过圆心的光滑圆槽,槽内有两根相同的橡皮绳拉住一质量为m的小球(可以视为质点),其中O点为圆盘中心,O′点为圆盘边缘.橡皮绳的劲度系数为k(类似弹簧遵从胡克定律),原长为圆半径R的1/3,现使圆盘的角速度由零开始缓慢增大,求圆盘的角速度为ω1=
与ω2=k 5m
时,小球所对应的线速度之比v1:v2.3k 5m
答案
设外面一根橡皮绳刚好松弛时圆盘的角速度为ω0,由牛顿第二定律:
k•
=mR 3
•ω 20
,2R 3
解得ω0=k 2m
当ω1=
时,两根橡皮绳都有拉力,设此时的半径为a,由牛顿第二定律:mk 5m
a=k(a-ω 21
)-k(R-a-R 3
),R 3
将ω1的值解得:a=
R5 9
当ω2=
时,外面一根橡皮绳已经松弛,设此时半径为b,由牛顿第二定律:3k 5m
m
b=k(b-ω 22
),R 3
将ω2的值代入解得:b=
,5R 6
则
=v1 v2
=ω1a ω2b 2 3 9
答:小球所对应的线速度之比v1:v2是2
:9.3
