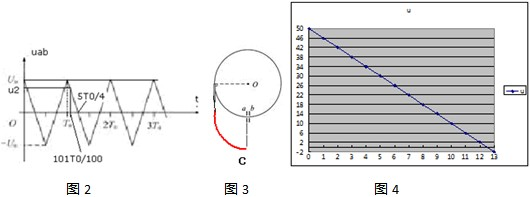
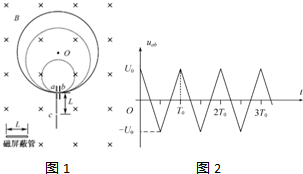
某种加速器的理想模型如图1所示:两块相距很近的平行小极板中间各开有一小孔a、b,两极板间电压uab的变化图象如图2所示,电压的最大值为U0、周期为T0,在两极板外有垂直纸面向里的匀强磁场.若将一质量为m0、电荷量为q的带正电的粒子从板内a孔处静止释放,经电场加速后进入磁场,在磁场中运动时间T0后恰能再次从a 孔进入电场加速.现该粒子的质量增加了m0.(粒子在两极板间的运动时间不计,两极板外无电场,不考虑粒子所受的重力)
(1)若在t=0时刻将该粒子从板内a孔处静止释放,求其第二次加速后从b孔射出时的动能;
(2)现在利用一根长为L的磁屏蔽管(磁屏蔽管置于磁场中时管内无磁场,忽略其对管外磁场的影响),使图1中实线轨迹(圆心为O)上运动的粒子从a孔正下方相距L处的c孔水平射出,请在答题卡图上的相应位置处画出磁屏蔽管;
(3)若将电压uab的频率提高为原来的2倍,该粒子应何时由板内a孔处静止开始加速,才能经多次加速后获得最大动能?最大动能是多少?
(1)质量为m0的粒子在磁场中作匀速圆周运动Bqv=,T0=
则T0=
当粒子的质量增加了m0,其周期增加△T=T0
根据题图2可知,粒子第一次的加速电压u1=U0
经过第二次加速,第2次加速电压u2,如图2
在三角形中,==,
所以粒子第二次的加速电压u2=U0
粒子射出时的动能 Ek2=qu1+qu2
解得Ek2=qU0
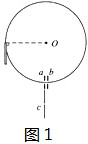
(2)因为磁屏蔽管使粒子匀速运动至以下L处,出管后仍然做圆周运动,可到C点水平射出.磁屏蔽管的位置如图1所示.粒子运动的轨迹如图3.
(3)如图4(用Excel作图)设T0=100,U0=50,得到在四分之一周期内的电压随时间变化的图象
从图象可以看出,时间每改变△t=(图象中为1),电压改变为U0(图象中为4),
所以图象中电压分别为50,46,42,38,…10,6,2,共13个,
设某时刻t,u=U0时被加速,此时刻可表示为•N,
静止开始加速的时刻t1为t1=•N-n×,其中n=12,将n=12代入得t1=•N-,
因为t1<,在u>0时,粒子被加速,则最多连续被加速的次数:N=,得N=25.
所以只能取N=25,解得t1=T0,由于电压的周期为,所以t=n+T0(n=0,1,2,3…)
故粒子由静止开始被加速的时刻t=(+)T0(n=0,1,2,…)
故加速时的电压分别U0,U0,U0…U0,U0,U0,
加速电压做的总功,即动能的最大值,故粒子的最大动能 Ekm=2×(++…)qU0+qU0
解得 Ekm=qU0.