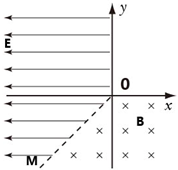
如图所示,在纸面内建立直角坐标系xOy,以第Ⅲ象限内的直线OM(与负x轴成45°角)和正y轴为界,在x<0的区域建立匀强电场,方向水平向左,场强大小E=0.32V/m;以直线OM和正x轴为界,在y<0的区域建立垂直纸面向里的匀强磁场,磁感应强度B=0.1T,一不计重力的带负电粒子,从坐标原点O沿y轴负方向以v0=2×103m/s的初速度射入磁场,已知粒子的比荷为q/m=5×106C/kg,求:
(1)粒子第一次经过磁场边界时的位置坐标
(2)粒子在磁场区域运动的总时间
(3)粒子最终离开电磁场区域时的位置坐标.
(1)粒子带负电,从O点沿y轴负方向射入磁场,沿顺时针方向做圆周运动.
第一次经过磁场边界上的一点(设为A点),
由qv0B=m
得:v02 r
r=
=4×10-3mmv02 qB
所以,A点的坐标为:(-4×10-3m,-4×10-3m)
(2)设粒子在磁场中做圆周运动的周期为T,第二次出磁场的点为C,第二次进入磁场的运动为
圆周,粒子在磁场中运动的总时间为:3 4
t=tOA+tAC=
T+1 4
T3 4
又 T=2πm qB
代入数据解得:T=1.265×10-5s,
所以t=1.265×10-5s
(3)粒子从C点沿y轴正方向进入电场,做类平抛运动,则
a=
,qE m
由平抛规律得:
△x=
at12=2r1 2
△y=v0t1
代入数据解得:△y=0.2m
y=△y-2r=0.2m-2×4×10-3m=0.192m
粒子离开电磁场时的位置坐标为:(0,0.192m).
答:(1)粒子第一次经过磁场边界时的位置坐标:(-4×10-3m,-4×10-3m)
(2)粒子在磁场区域运动的总时间1.265×10-5s
(3)粒子最终离开电磁场区域时的位置坐标(0,0.192m)

