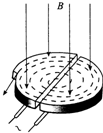
回旋加速器是用来加速带电粒子的装置,如图所示.它的核心部分是两个D形金属盒,两盒相距很近(缝隙的宽度远小于盒半径),分别和高频交流电源相连接,使带电粒子每通过缝隙时恰好在最大电压下被加速.两盒放在匀强磁场中,磁场方向垂直于盒面,带电粒子在磁场中做圆周运动,粒子通过两盒的缝隙时反复被加速,直到最大圆周半径时通过特殊装置被引出.若D形盒半径为R,所加磁场的磁感应强度为B.设两D形盒之间所加的交流电压的最大值为U,被加速的粒子为α粒子,其质量为m、电量为q.α粒子从D形盒中央开始被加速(初动能可以忽略),经若干次加速后,α粒子从D形盒边缘被引出.求:
(1)α粒子被加速后获得的最大动能Ek;
(2)α粒子在第n次加速后进入一个D形盒中的回旋半径与紧接着第n+1次加速后进入另一个D形盒后的回旋半径之比;
(3)α粒子在回旋加速器中运动的时间;
(4)若使用此回旋加速器加速氘核,要想使氘核获得与α粒子相同的动能,请你通过分析,提出一个简单可行的办法.
(1)α粒子在D形盒内做圆周运动,轨道半径达到最大时被引出,具有最大动能.设此时的速度为v,有 qvB=mv2 R
可得v=qBR m
α粒子的最大动能Ek=
mv2=1 2 q2B2R2 2m
(2)α粒子被加速一次所获得的能量为qU,α粒子被第n次和n+1次加速后的动能分别为
EKn=
mvn2=1 2
=nqU q2B2Rn2 2m
EKn+1=
mvn+12=1 2
=(n+1)qU q2B2Rn+12 2m
可得
=Rn Rn+1 n n+1
(3)设α粒子被电场加速的总次数为a,则
Ek=aqU=q2B2R2 2m
可得 a=qB2R2 2mU
α粒子在加速器中运动的时间是α粒子在D形盒中旋转a个半圆周的总时间t.
t=aT 2
T=2πm qB
解得
t=πBR2 2U
(4)加速器加速带电粒子的能量为Ek=
mv2=1 2
,由α粒子换成氘核,有q2B2R2 2m
=q2B2R2 2m
,则B1=(
)2B12R2q 2 2(
)m 2
B,即磁感应强度需增大为原来的2
倍;2
高频交流电源的周期T=
,由α粒子换为氘核时,交流电源的周期应为原来的2πm qB
倍.2 2
