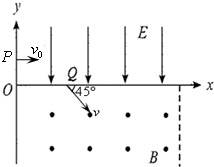
如图,在xoy平面第一象限整个区域分布匀强电场,电场方向平行y轴向下,在第四象限内存在有界匀强磁场,左边界为y轴,右边界为x=
d的直线,磁场方向垂直纸面向外.质量为m、带电量为+q的粒子从y轴上P点以初速度v0垂直y轴射入匀强电场,在电场力作用下从x轴上Q点以与x轴正方向成45°角进入匀强磁场.已知OQ=d,不计粒子重力.求:5 2
(1)P点坐标;
(2)要使粒子能再进入电场,磁感应强度B的取值范围;
(3)要使粒子能第二次进入磁场,磁感应强度B的取值范围.
(1)设粒子进入电场时y方向的速度为vy,则vy=v0tan45°
设粒子在电场中运动时间为t,则
OQ=v0t
OP=
tvy 2
由以上各式,解得OP=
P点坐标为(0,d 2
)d 2
(2)粒子刚好能再进入电场的轨迹如图所示,设此时的轨迹半径为r1,则
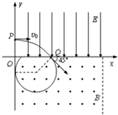
r1+r1sin45°=d 解得:r1=(2-
)d2
令粒子在磁场中的速度为v,则v=v0 cos45°
根据牛顿第二定律qvB1=
解得:B1=mv2 r1 (
+1)mv02 qd
要使粒子能再进入电场,磁感应强度B的范围 B≥B1
要使粒子刚好从x=2.5d处第二次进入磁场的轨迹如图,
粒子从P到Q的时间为t,则粒子从C到D的时间为2t,所以 CD=2d
CQ=CD-QD=2d-(2.5d-d)=d 2
设此时粒子在磁场中的轨道半径为r2,由几何关系 2r2sin45°=CQ解得 r2=
d 2 4
根据牛顿第二定律 qvB2=
解得B2=mv2 r2 4mv0 qd
要使粒子能第二次进磁场,粒子必须先进入电场,故磁感应强度B要满足B≤B2
综上所述要使粒子能第二次进磁场,磁感应强度B要满足
≤B≤(
+1)mv02 qd 4mv0 qd
答:(1)P点的坐标为(0,
)d 2
(2)要使粒子能再进入电场,磁感应强度B的取值范围B≥(
+1)mv02 qd
(3)磁感应强度B要满足
≤B≤(
+1)mv02 qd 4mv0 qd
