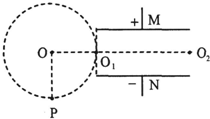
如图所示,在真空中,半径为d的虚线所围的圆形区域内只存在垂直纸面向外的匀强磁场,在磁场右侧有一对平行金属板M和N,两板间距离也为d,板长为l.板
间存在匀强电场,两板间的电压为U0.两板的中心线O1O2,与磁场区域的圆心O在同一直线上.有一电荷量为q、质量为m的带正电粒子,以速率v0从圆周上的P点沿垂直于半径OOl并指向圆心O的方向进入磁场,从圆周上的O1点飞出磁场后沿两板的中心线O1O2射入匀强电场,从两板右端某处飞出.不计粒子所受重力.求
(1)磁场的磁感应强度B的大小
(2)粒子在磁场和电场中运动的总时间
(3)当粒子在电场中经过时间t=
时,突然改变两金属板带电性质,使电场反向,且两板间电压变为U1,则粒子恰好能从O2点飞出电场,求电压U1和U0的比值.l 2v0
(1)粒子在磁场中做匀速圆周运动,设圆周运动的半径为r,由牛顿第二定律
qv0B=mv 20 r
由几何关系知 r=d
所以 B=mv0 qd
(2)粒子在磁场中运动的周期T=
,2πm qB
在磁场中运动时间为四分之一个周期,t1=
T=1 4
•1 4
=2πm qB
.πl 2v0
粒子在电场中做类平抛运动,平行板的方向做匀速直线运动
则t2=l v0
在电磁场中运动的总时间t总=t1+t2=πl+2l 2v0
(3)根据运动的独立性可知:粒子在竖直方向先做匀加速直线运动,再做等时间的匀减速直线运动,
第一阶段:a=
,s=qU0 md
at21 2
第二阶段:a1=
,s1=vt-qU1 md
a1t2=at2-1 2
a1t21 2
竖直方向总位移为零,s+s1=0
所以解得 a1=3a
故U1:U0=3:1
答:(1)磁场的磁感应强度B的大小是
.mv0 qd
(2)粒子在磁场和电场中运动的总时间是
.πl+2l 2v0
(3)电压U1和U0的比值是3:1.
