问题
选择题
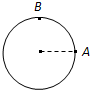
如图所示,质量为m的小球在竖直面内的光滑圆轨道内侧做半径为R的圆周运动,不计空气阻力,设小球恰好能通过最高点B时速度的大小为v.若小球在最低点以大小为2v的速度水平向右运动,则下列说法正确的是( )
A.小球在最低点对轨道的压力大小为5mg
B.小球能通过轨道的最高点B
C.小球不能通过轨道上与圆心等高的A点
D.小球在AB之间某一点脱离圆轨道,此后做平抛运动
答案
A、在最低点,根据牛顿第二定律得,N-mg=m
,又v2=gR,解得N=5mg,所以小球在最低点对轨道的压力为5mg.故A正确,4v2 R
B、在最高点有:mg═m
由机械能守恒定律得,v2 R
m(2v)2=mg•2R+1 2
mv′2,联立两式解得v′=0,则小球不能通过最高点,故B错误.1 2
C、当小球运动到与圆心等高处时,根据机械能守恒定律得,
m(2v)2=mg•R+1 2
mv″2,又v2=gR,解得v″=1 2
v>0,所以小球能通过与圆心等高处.故C错误.2
D、小球在AB之间某一点脱离圆轨道,做向心运动,导致小球做斜抛运动.故D错误.
故选A.
