在平面直角坐标系xOy中，第I象限存在沿y轴负方向的匀强电场，第I

问题问答题

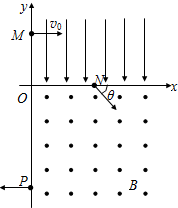
在平面直角坐标系xOy中，第I象限存在沿y轴负方向的匀强电场，第IV象限存在垂直于坐标平面向外的匀强磁场，磁感应强度大小为B．一质量为m，电荷量为q的带正电的粒子从y轴正半轴上的M点以速度v₀垂直于y轴射入电场，经x轴上的N点与x轴正方向成θ=60°角离开电场，同时射入磁场，最后从y轴负半轴上的P点垂直于y轴射出磁场，如图所示．（不计粒子重力）试求：

（1）粒子离开电场时的速度大小；

（2）M、N两点间的电势差U_MN；

（3）P点到坐标原点O的距离OP．

答案

（1）

粒子垂直于电场进入第一象限，粒子做类平抛运动，将到达N点的速度分解得知

vcosθ=v₀，

解得，粒子离开电场时的速度大小v=2v₀．

（2）从M→N过程，由动能定理得

qU_MN=

mv2-

代入解得，U_MN=

（3）粒子进入第四象限后，在洛伦兹力的作用下做匀速圆周运动，则

qvB=m

得粒子在磁场中做圆周运动的轨道半径为 R=

2mv0

．

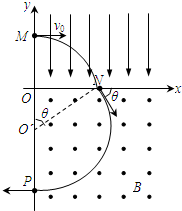
画出轨迹如图，由几何知识得

OP=R+Rcosθ=

3mv0

答：

（1）粒子离开电场时的速度大小是2v₀；

（2）M、N两点间的电势差U_MN为

．

（3）P点到坐标原点O的距离OP是

3mv0

．