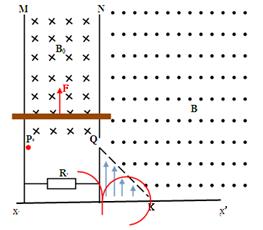
如图所示,水平面xx´上竖直放着两根两平行金属板M、N,板间距离为L=1m,两板间接一阻值为2Ω的电阻,在N板上开一小孔Q,在M、N及Q上方有向里匀强磁场B0=1T;在Nx´范围内有一450分界线连接Q和水平面,NQ与分界线间有向外的磁感应强度B=0.5T的匀强磁场;N、水平面及分界线间有竖直向上的电场;现有一质量为0.2㎏的金属棒搭在M、N之间并与MN良好接触,金属棒在MN之间的有效电阻为1Ω,M、N电阻不计,现用额定功率为P0=9瓦的机械以恒定加速度a=1m/s2匀加速启动拉着金属棒向上运动,在金属棒达最大速度后,在与Q等高并靠近M板的P点释放一个质量为m电量为+q的离子,离子的荷质比为20000C/㎏,求:

(1)金属棒匀加速运动的时间。(结果保留到小数点后一位)
(2)离子刚出Q点时的速度。
(3)离子出Q点后,在竖直向上的电场作用下,刚好能打到分界线与水平面的交点K,过K后再也不回到磁场B中,求Q到水平面的距离及离子在磁场B中的运动时间。
(1)t=2.9秒 (2)v=200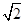 m/s (3)6.28×10-4s
m/s (3)6.28×10-4s
(1)设匀中速时间为t.
V=at……….①
F安=B0IL...........②
I= ............③
............③
F-Mg-F安=Ma........④
FV=P0......................⑤
联立以上各式得t=2.9秒
(2)设棒匀速运动时的速度为V0
FV0=P0.........⑥
F=Mg+F安................⑦
F安=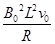 .............⑧
.............⑧
联立以上三式得:V0=3m/s
些时的感应电动势ε=B0LV0=3伏,UMN=2伏
由动能定理: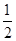 mv2=qUMN 得v=200
mv2=qUMN 得v=200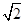 m/s
m/s
(3)如图,离子在B和电场中的运动轨迹如图所示:
由几何知识可知,离子运动的轨道半径r=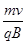 ...........⑨.
...........⑨.
Q到平面的距离h=2r.............⑩
联立..⑨和⑩得h=4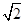 ×10-2m/s
×10-2m/s
t´=T=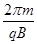 =6.28×10-4s
=6.28×10-4s