在真空室内取坐标系xOy,在x轴上方存在二个方向都垂直于纸面向外的磁场区Ⅰ和Ⅱ(如图),平行于x轴的虚线MM’和NN’是它们的边界线,两个区域在y方向上的宽度都为d、在x方向上都足够长.Ⅰ区和Ⅱ区内分别充满磁感应强度为B和
B的匀强磁场.一带正电的粒子质量为m、电荷量为q,从坐标原点O以大小为v的速度沿y轴正方向射入Ⅰ区的磁场中.不计粒子的重力作用.2 3
(1)如果粒子只是在Ⅰ区内运动而没有到达Ⅱ区,那么粒子的速度v满足什么条件?粒子运动了多长时间到达x轴?
(2)如果粒子运动过程经过Ⅱ区而且最后还是从x轴离开磁场,那么粒子的速度v又满足什么条件?并求这种情况下粒子到达x轴的坐标范围?
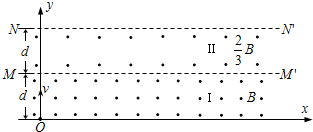
粒子恰好没有到达M的轨迹如图,则:R=d
由洛伦兹力提供向心力:qvB=mv2 R
得:v=qBd m
粒子只是在Ⅰ区内运动而没有到达Ⅱ区,粒子的速度应满足:v≤qBd m
又根据T=
及t=2πR v T 2
得:t=πm qB
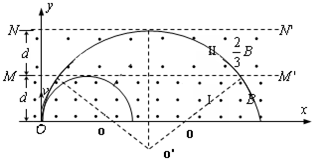
(2)粒子经过Ⅱ区而且刚好能从x轴离开磁场的轨迹如图
依题意,有 qvB=
及 qvmv2 R1
B=2 3 mv2 R2
由几何关系得:
=R2-d d R2 R1
整理得:v=5qBd 3m
设此时粒子离开磁场的坐标为L,则L=2R1+2(R2-R1)2-(R2-2d)2
联立以上3个公式,整理得:L=
d14 3
故粒子速度应满足:
<v≤qBd m 5qBd 3m
粒子到达x轴的坐标范围为:2d<x≤
d14 3
答:(1)粒子的速度v满足:v≤
粒子运动的时间:t=qBd m
;(2)该情况下粒子的速度v又满足:πm qB
<v≤qBd m
;粒子到达x轴的坐标范围为:2d<x≤5qBd 3m
d14 3
