问题
问答题
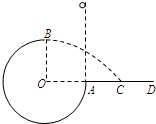
如图所示,竖直平面内的3/4圆弧形光滑轨道半径为R,A端与圆心O等高,AD为水平面,B端在O的正上方,一个小球在A点正上方由静止释放,自由下落至A点进入圆轨道并恰能到达B点.
求:(1)释放点距A点的竖直高度;
(2)落点C与O点的水平距离.
答案
(1)设小球距A点高为h处下落,到达B点时速度大小为vB.小球下落过程只有重力做功,故小球由最高点经A运动B点过程中机械能守恒:
mg(h-R)=
mvB2 ①1 2
由圆周运动规律可知,小球恰能达到B点的最小速度的条件为:
mg=m
②vB2 R
由①②解得:h=
R 3 2
(2)设小球由B点运动到C点所用的时间为t,小球离开B点后做平抛运动,设落点C与O点的水平距离为S,则有:
S=vBt ③
R=
gt2 ④1 2
由②③④解得:S=
R 2
所以落点C与A点的水平距离x=(
-1)R2
答:(1)释放点距A点的竖直高度为
R;3 2
(2)落点C与O点的水平距离为(
-1)R.2
