问题
问答题
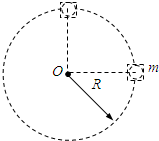
如图所示,质量为m的小球置于正方体的光滑盒子中,盒子的边长略大于球的直径.某同学拿着该盒子在竖直平面内做半径为R的匀速圆周运动,已知重力加速度为g,空气阻力不计,问:
(1)要使盒子在最高点时盒子与小球之间恰好无作用力,则该盒子做匀速圆周运动的周期为多少?
(2)若盒子以第(1)问中周期的
做匀速圆周运动,则当盒子运动到图示球心与O点位于同一水平面位置时,小球对盒子的哪些面有作用力,作用力为多大?1 2
答案
(1)设此时盒子的运动周期为T0,因为在最高点时盒子与小球之间刚好无作用力,因此小球仅受重力作用.根据牛顿运动定律得:
mg=mv2 R
又周期T0=2πR v
解之得:T0=2πR g
(2)设此时盒子的运动周期为T,则此时小球的向心加速度为:an=
R4π2 T2
由第一问知:g=
R 且T=4π2 T02 T 0 2
由上述三式知:an=4g
设小球受盒子右侧面的作用力为F,受上侧面的作用力为N,根据牛顿运动定律知:
在水平方向上:F=man
即:F=4mg
在竖直方向上:N+mg=0
即:N=-mg
因为F为正值、N为负值,所以小球对盒子的右侧面和下侧面有作用力,分别为4mg和mg.
答:(1)该盒子做匀速圆周运动的周期为2π
.R g
(2)小球对盒子的右侧面和下侧面有作用力,分别为4mg和mg.
