用一根长L=0.8m的轻绳,吊一质量为m=1.0g的带电小球,放在磁感应强度B=0.1T,方向如图所示的匀强磁场中,把小球拉到悬点的右端,轻绳刚好水平拉直,将小球由静止释放,小球便在垂直于磁场的竖直平面内摆动,当小球第一次摆到低点时,悬线的拉力恰好为零(重力加速度g取10m/s2).试问:
(1)小球带何种电荷?电量为多少?
(2)当小球第二次经过最低点时,悬线对小球的拉力多大?
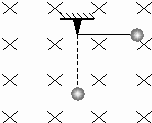
(1)小球第一次摆到最低点时速度水平向左,悬线的拉力恰好为零,说明洛伦兹力竖直向上,由左手定则,拇指向上,让磁感线穿过掌心,四指就指向右,故小球带负电.
下落的过程中只有重力做功,洛伦兹力不做功,所以总功为:mgL
设小球第一次到达最低点速度为v,则由动能定理可得:
mgL=
mv21 2
在最低点由向心力公式得:Bqv-mg=mv2 L
解得q=7.5×10-2C
(2)小球第二次到达最低点速度仍为v,
向心力公式得:F-Bqv-mg=mv2 L
解得F=0.06N
答:(1)小球带负电荷,电量为7.5×10-2C;
(2)当小球第二次经过最低点时,悬线对小球的拉力为0.06N.
