问题
问答题
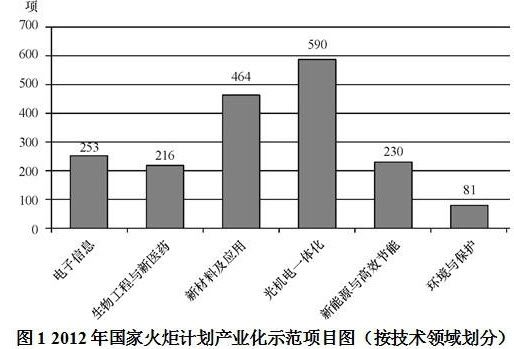
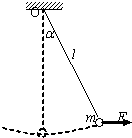
如图所示，长度为L的轻绳上端固定在O点，下端系一质量为m的小球（小球的大小可以忽略）．已知重力加速度为g．
（1）在水平拉力F的作用下，轻绳与竖直方向的夹角为α，小球处于平衡状态．求力F的大小；
（2）由图示位置无初速释放小球，求当小球第一次通过最低点时的速度及轻绳对小球的拉力（不计空气阻力）．
答案
（1）根据平衡条件，应满足Tcosα=mg，Tsinα=F，
拉力大小F=mgtanα；
（2）运动中只有重力做功，根据机械能守恒：mgl（1-cosα）=
mv2，1 2
则通过最低点时：小球的速度大小v=
，2gl(1-cosα)
方向水平向左；
根据牛顿第二定律：T-mg=m
，v2 l
绳子对小球的拉力：T=mg+m
=mg（3-2cosα），v2 l
方向竖直向上．
答：（1）力F的大小为mgtanα．
（2）小球第一次通过最低点时的速度v=
，轻绳对小球的拉力mg（3-2cosα）．2gl(1-cosα)
（）