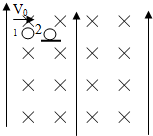
如图所示,在足够大的空间范围内,同时存在着竖直向上的匀强电场和垂直纸面向里的水平匀强磁场,磁感应强度B=1.57T.小球1带正电,其电量与质量之比q1/m1=4C/kg,所受重力与电场力的大小相等;小球2不带电,静止放置于固定的水平悬空支架上.小球向右以v0=23.59m/s的水平速度与小球2正碰,碰后经过0.75s再次相碰.设碰撞前后两小球带电情况不发生改变,且始终保持在同一竖直平面内.(取g=10m/s2)
问:(1)电场强度E的大小是多少?
(2)两小球的质量之比
是多少?m2 m1
(1)小球1所受的重力与电场力始终平衡 m1g=q1E ①
解得E=2.5 N/C ②
电场强度为2.5N/C;
(2)相碰后小球1做匀速圆周运动,由牛顿第二定律得:
q1v1B=m1
③v 21 R1
半径为R1=
④m1v1 q1B
周期为T=
=1 s ⑤2πm1 q1B
∵两小球运动时间t=0.75s=
T3 4
∴小球1只能逆时针经
个圆周时与小球2再次相碰 ⑥3 4
第一次相碰后小球2作平抛运动 h=R2=
gt2 ⑦1 2
L=R1=v1t ⑧
两小球第一次碰撞前后动量守恒,以水平向右为正方向
m1v0=-m1v1+m2v2 ⑨
由⑦、⑧式得v2=3.75 m/s
由④式得v1=
=66 m/sq1BR1 m1
∴两小球质量之比
=m2 m1
=11⑩v0+v1 v2
故两小时球质量之比为11.
