问题
填空题
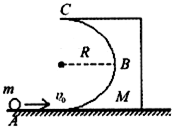
如图所示,质量M,半径R的光滑半圆槽第一次被固定在光滑水平地面上,质量为m的小球,以某一初速度冲向半圆槽刚好可以到达顶端C.然后放开半圆槽.其可以自由运动,m小球又以同样的初速冲向半圆槽,小球最高可以到达与圆心等高的B点,(g=10m/s2)
试求:
①半圆槽第一次被固定时,小球运动至C点后平抛运动的水平射程X=?
②小球质量与半圆槽质量的比值m/M为多少?
答案
①小球刚好可以到达顶端C,说明刚好由重力提供向心力
mg=mv12 R
所以到达C点时的速度为v1=gR
小球由C点做平抛运动
竖直方向上的位移y=2R=
gt21 2
所以运动的时间为t=4R g
水平方向上的位移x=v1t=
•gR
=2R4R g
②半圆槽第一次被固定时,对小球运用动能定理-2mgR=
mv12-1 2
mv021 2
解得v02=5gR
然后放开半圆槽后,m小球又以同样的初速冲向半圆槽,
对m、M系统根据动量守恒定律:
mv0=(m+M)v2
所以v2=
=mv0 m+M m m+M 5gR
对m、M系统根据动能定理有:
-mgR=
(m+M)v22-1 2
mv021 2
所以-mgR=
(m+M)•(1 2 m m+M
)2-5gR
m•5gR1 2
化简得
=m M 3 2
答:①半圆槽第一次被固定时,小球运动至C点后平抛运动的水平射程X=2R.
②小球质量与半圆槽质量的比值为
=m M
.3 2

