问题
问答题
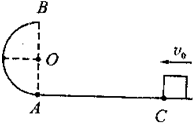
如图所示,半径R=0.40m的光滑半圆环轨道处于竖直平面内,半圆环与粗糙的水平地面相切于圆环的端点A.一质量m=0.10kg的物块(可以看成质点),在离A点4.0m处的C点以初速度V0冲向圆环,要求物块在圆环上运动的过程中不脱离圆环,那么对初速度V0有什么要求?(已知物块与地面间的动摩擦因数μ=0.2,取g=10m/s2)
答案
运动时最高点不超过D点(D点是与圆心O等高的环上的一点),对于这种情况:要物块不离开圆环,则vD=0,或到不了D点,
根据动能定理,则有:
m1 2
-v 2D
m′1 2
=-μmgLAC-mgRv 20
解得:v0≤2
m/s6
当运动到最高点B点时,则最高点的速度不能低于
,才能不离开圆环,gR
对物块从C到B过程,根据动能定理,
则有:
m1 2
-v 2B
m1 2
=-μmgLAC-mghABv 20
代入数据,解得:v0≥6m/s,
综合所述,则有:v0≥6m/s 或 v0≤2
m/s.6
答:要求物块在圆环上运动的过程中不脱离圆环,那么对初速度V0有:v0≥6m/s 或 v0≤2
m/s.6
