如图所示,一束具有各种速率的带一个基本正电荷的两种铜离子,质量数分别为63和65,水平的经小孔 S 进入有匀强电场和匀强磁场的区域.电场 E 的方向向下,磁场B的方向垂直纸面向里.只有那些路径不发生偏折的离子才能通过另一个小孔S′.为了把从S′射出的两种铜离子分开,再让它们进入另一方向垂直纸面向外的匀强磁场B′中,使两种离子分别沿不同半径的圆形轨道运动.试分别求出两种离子的轨道半径.
(已知E=1.00×105V/m,B=0.4T,B′=0.50T,基本电荷e=1.60×10-19C,质量数为63的铜原子的质量m1=63×1.66×10-27kg,质量数为65的铜原子的质量m2=65×1.66×10-27kg)
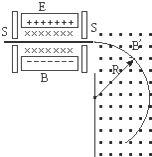
(1)设铜离子的电量为e,以速度v进入小孔S后,
受到的力有电场力F1=Ee,方向向下
洛仑兹力F2=evB,方向向上
重力可忽略不计,只有当F1=F2时,铜离子才能匀速无偏折地穿出小孔S'.因此,从小孔S'穿出的铜离子必须满足的条件是
eE=evB--------------(1)
这就是说,只有速度v=
的铜离子能穿出小孔S'.E B
(2)铜离子进入磁场B'后,受到洛仑兹力F=evB',重力仍可忽略不计.F跟v垂直并为一恒量,因此铜离子在磁场B'内将作匀速圆周运动,
F就是这种圆周运动的向心力
设铜63离子和铜65离子运动轨迹的半径分别为R1和R2,那么evB′=
---------(2)m1v2 R1
evB′=
--------(3)m2v2 R2
(3)由(1)、(2)两式可得:
R1=
------------(4)m1E eBB′
由(1)、(3)两式可得:
R2=
---------(5)m2E eBB′
代入数值进行计算,
R1=
m=0.33m63×1.66×1027×1.00×105 1.60×10-19×0.40×0.50
R2=
m=0.34m65×1.66×1027×1.00×105 1.60×10-19×0.40×0.50
答:两种离子的轨道半径分别是:0.33m和0.34m.
