问题
问答题
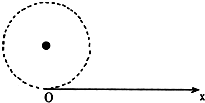
真空中有一半径r的圆柱形匀强磁场区域,磁场方向垂直于纸面向里.OX为过边界上
O点的切线,如图所示,从O点在纸面内向各个方向发射速率均为v0的电子,设电子间相互作用忽略,且电子在磁场中的偏转半径也为r.已知电子的电荷量为e,质量为m.
(1)求磁感应强度B;
(2)速度方向分别与OX方向夹角成60°和90°的电子,在磁场中的运动时间分别为多
少?
(3)所有从磁场边界出射的电子,速度方向有何特征?
答案
(1)由qvB=m
得 B=v2 r
.mv qr
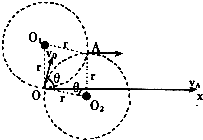
(2)如图,人射时电子速度与x轴夹角为θ,无论入射的速度方向与X轴的夹角为何值.由人射点O,射出点A,磁场圆心O1和轨道圆心O2一定组成边长为r的菱形,因O1O⊥OX,OO2垂直于入射速度,故∠OO2A=θ,即电子在磁场中所偏转的角度一定等于入射时电子速度与OX轴的夹角.
当 θ=60°时,t1=
=T 6
.π-R 3v
当 θ=90°时,t2=
=T 4 π-R 2v
(3)因∠OO2A=θ,故O2A⊥OX.而O2A与电子射出的速度方向垂直,可知电子射出方向一定与OX轴方向平行,即所有的电子射出圆形磁场时,速度方向均与OX轴相同.
答:
(1)磁感应强度B为
;mv qr
(2)速度方向分别与OX方向夹角成60°和90°的电子,在磁场中的运动时间分别为
,π-R 3v
.π-R 2v
(3)所有从磁场边界出射的电子,所有的电子射出圆形磁场时,速度方向均与OX轴相同.
