如图,竖直平面内有一直角坐标系xOy,在x≥0的区域内有一倾角为45°的绝缘光滑斜面,斜面末端O处用一极小的平滑曲面连接,恰能使斜面末端水平.在x≤0的广泛区域内存在正交的匀强磁场和匀强电场,磁场垂直于纸面向里,磁感应强度大小为B;电场沿竖直方向,场强大小为E.电荷量为-q的带电小球从绝缘光滑斜面上某点由静止开始下滑,小球经斜面末端O点进入电场和磁场,之后沿圆周运动,垂直于y轴离开电场和磁场,最后垂直打到斜面上.
求:
(1)小球从开始运动到垂直打到斜面上所用时间.
(2)小球开始下滑的初始位置坐标.
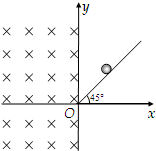

(1)小球运动的轨迹如图.初始位置(x1,y1),再次回到斜面的落点位置(x2,y2),小球经时间t1运动到末端的速度为v0,则
t1=
①v0 gsin45°
小球在复合场中做匀速圆周运动,则有 mg=qE ②
轨道半径为 r=
③mv0 qB
运动时间为 t2=
T=1 2
④πm qB
小球离开电磁场后做平抛运动,经时间t3垂直落到斜面时
v0=vytan45°=gt3 ⑤
2r-y2=
g1 2
⑥t 23
y2=x2=v0t3,⑦
由②③⑤⑥⑦得,t3=
⑧v0=4E 3gB
⑨4E 3B
由②④得,t2=
⑩πE gB
由①⑨得,t1=4
E2 3gB
故小球从开始运动到垂直打到斜面上所用时间为t=t1+t2+t3=(
+π)4(
+1)2 3
.E gB
(2)小球初始位置到斜面末端的距离为 l=
gsin45°1 2
=t 21 8
E22 9gB2
故 x1=y1=lsin45°=8E2 9gB2
答:
(1)小球从开始运动到垂直打到斜面上所用时间为(
+π)4(
+1)2 3
..E gB
(2)小球开始下滑的初始位置坐标(
,8E2 9gB2
).8E2 9gB2
